この記事のもくじ
まえがき
今更だけど、一応紹介
という位置づけです。「資産運用は複利が効くから優れているんだ!」とか「時間をかけることで複利の力が働く」ということは投資を始めれば耳タコで耳にする情報です。
そもそも投資の世界は銀行預金みたいに毎年の利回りが一定ではないので「利益が利益を産んでいる、とは言えない場合もあるのにコレって複利?」というツッコミ考えを持たれている方、一旦それは無視でお願いします。
ということで株や債券への投資では複利が効くという前提の元では指数関数的に資産価値は増加して行きます。
利回り1%なら倍になるのに単利なら100年・・・と思いきや72年、2%なら50年と思いきや36年で倍になるというのです。特に株の世界だと大体10年で2倍になると言われていますがコレは全世界に投資していたら利回りが7%だから。
この倍になるまでの期間を概算するために使われているのが72の法則です。
今回はこの72の法則についての紹介です。
72の法則はこんなにシンプル

数式が苦手な人でも大丈夫。たったコレだけの数式です。
- 元本が倍になるまでの年数=72/利回り
先ほど紹介した1%なら72年、2%なら36年で倍になるというのはこの式に利回りを当て込んでいるだけです。72の法則はグラフで書くとこんな感じ。小学校だか中学校で習う「反比例」のグラフになります。
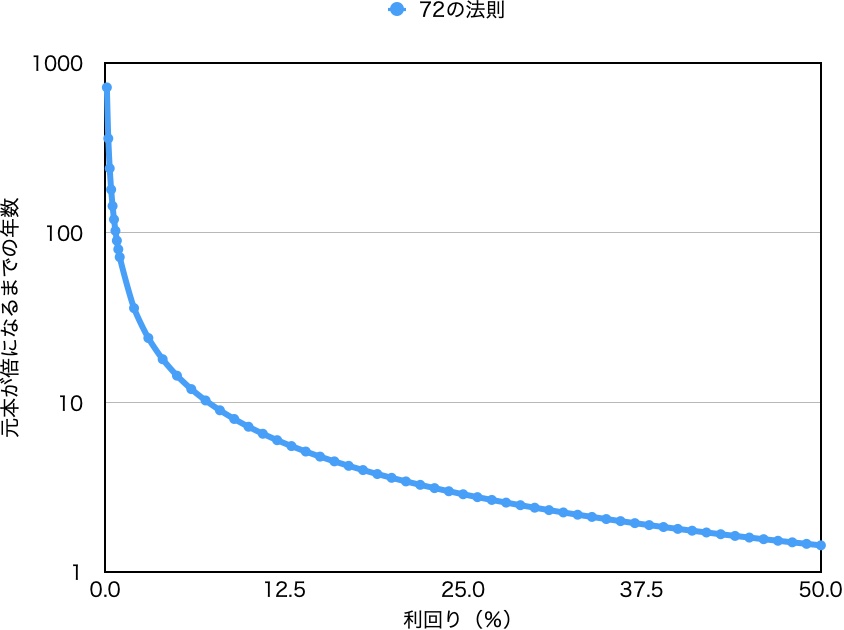
左側に行けば行くほど急峻に倍になるまでの年数が増えてます。銀行預金の中で高利率と言われる楽天銀行(300万円までは0.1%)、あおぞら銀行(0.2%)でも倍になるのはそれぞれ720年、360年です。「投資が怖いから〜」とせっせと預金だけしていると大きく増えることはないのは実感でも上図でも理解してもらえるかと思います。
72の法則って正しいの?

厳密に元本が倍になる年数を求める方法
あくまで72の法則は概算するための数式です。となると「じゃあ実は厳密に必要な年数を計算したら72の法則とずれるとこ路があるのでは?」と思うのでは。自分は思いました。
ということで正確な計算式との対比をしてみることにしました。
厳密にはこのように求められます。aの部分が利回りで1%なら0.01、10%なら0.1と入れればxに年数が出てきます。
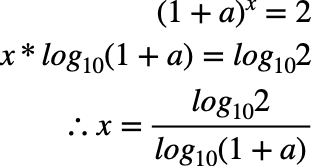
指数対数がわからない!という方は別個で勉強してくださいませm(_ _)m
この式をもとに先ほどと同じようなグラフを作るとこうなります。
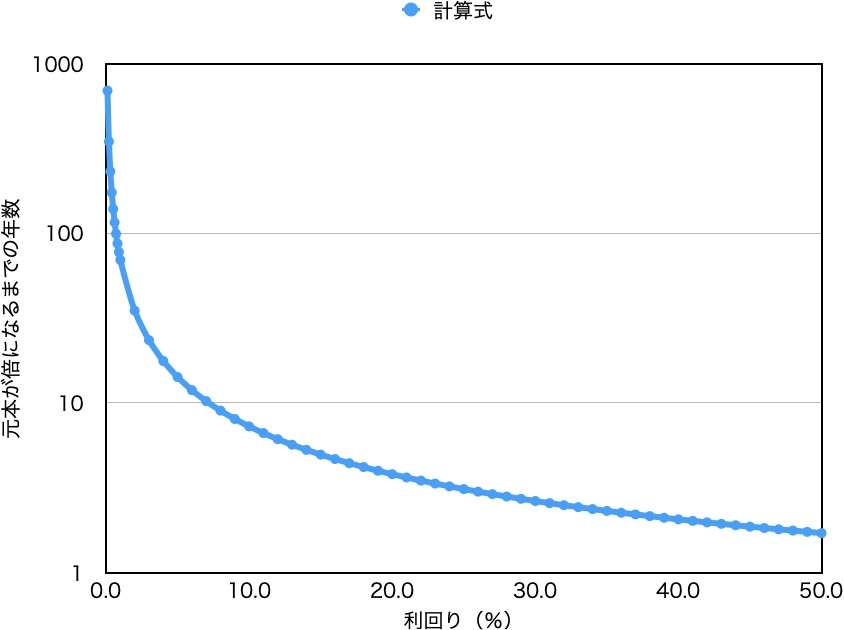
う〜ん、形は似てますね。そりゃ似てないと72の法則が嘘つきってことにはなるんですけど。
2つを重ね合わせると
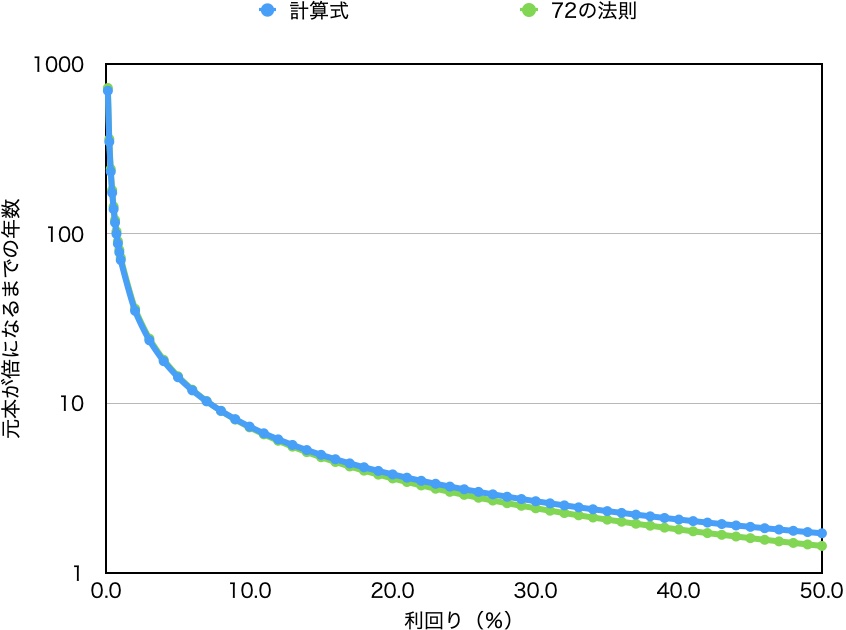
ほぼ一緒です。利回りが高い場合は72の法則の方が厳密な年数よリモ短く見込んでいますが、こんな利回りが高いことは現実にはほぼ起こらないので問題なしです。
利回りが低い場合はずれでいうと1年以内(0.何年というレベルのずれ)なので何の心配もなく72の法則を使えば概算どころかかなり正確に見通しは立てられるってことになります。
ぱっと見難しい数式でないと厳密に求められないところを実用上の範囲では72/利回りというシンプルな数式で表現できてしまうのは面白いポイントです。
あとがき
冒頭でも書いたように、株式や債券は価格の動きが必ず1%とか6%と確約されているわけではなくて結果的に振り返ってみたら1年当たり〜%だった、というのにすぎません。
なので複利の考え方通りになっているのかと言ったら自分はNOだと思ってますが長期的には当てはまるような値動き(上がったり下がったりはするけど結局10年後に倍になってた的な)にはなるわけですので資産運用の計画を立てる上で72の法則は有効なツールと言えますね。




